Tugas Mandiri II – Teknik Kompilasi

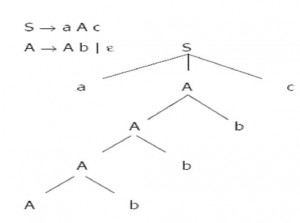
Left Recursive dan Left Factoring

Pada top down parsing tidak diperbolehkan adanya left recursive serta grammar yang akan di parsing harus di left-factored (menggunakan metode left-factoring) karena :

1. Grammar yang memiliki left recursive tidak bisa diperiksa, sehingga harus diubah dulu agar tidak left recursive lagi. Karena left recursive akan mengakibatkan loop yang terus-menerus .

Contoh grammar yang memiliki left recursive :

Dari contoh di atas, dapat kita lihat bahwa grammar tersebut mengalami loop yang terus menerus. Oleh karena itu, untuk menghindari penurunan kiri yang looping, perlu dihilangkan sifat rekursif, dengan langkah-langkah sebagai berikut :

Pisahkan Aturan produksi yang rekursif kiri dan yang tidak.

Aturan produksi yang rekursif kiri :

A -> A α1 | A α2 | … | A αn

Aturan produksi yang tidak rekursif kiri

A -> β1 | β2 | … | βn

Lakukan pergantian aturan produksi yang rekursif kiri, sebagai berikut :

1. A -> β1 Z | β2 Z | … | βn Z

2. Z -> α1 | α2 | … | αn

3. Z -> α1 Z | α2 Z | … | αn Z

Pergantian dilakukan untuk setiap aturan produksi dengan simbol ruas kiri yang sama, bisa diganti dengan variabel Z1, Z2 dst, sesuai dengan variabel yang menghasilkan rekurisif kiri.

Contoh :

S -> Sab | aSc | dd | ff | Sbd

Pisahkan aturan produksi yang rekursif kiri

S -> Sab | Sbd

Ruas Kiri untuk S: α1=ab , α2=bd

Aturan Produksi yang tidak rekursif kiri

S -> aSc | dd | ff

Dari situ didapat untuk Ruas Kiri untuk S: β1 = aSc, β2 = dd, β3= ff

Langkah berikutnya adalah penggantian yang rekursif kiri

S -> Sab | Sbd, dapat digantikan dengan

1. S -> aScZ1 | ddZ1 | ffZ1

2. Z1 -> ab | bd

3. Z1 -> abZ1 | bdZ1

Hasil akhir yang didapat setelah menghilangkan rekursif kiri adalah sebagai berikut :

S -> aSc | dd | ff

S -> aScZ1 | ddZ1 | ffZ1

Z1 -> ab | bd

Z1 -> abZ1 | bdZ1

2. Grammar yang belum di left-factored menggunakan left-factoring maka akan mengakibatkan konflik First-first yaitu konflik dimana susah untuk menentukan First dari suatu variable dalam grammar karena memiliki 2 produksi yang dimulai dengan terminal yang sama (mengakibatkan suatu grammar ambigu) sehingga dapat digunakan left-factoring untuk menghilangkan keambiguan dalam grammar tersebut.

Contoh grammar yang memiliki konflik first-first:

E → T + E | T

T → int | int * T | ( E )

Penjelasan:

First(E) adalah T dimana ada 2 produksi E yang dimulai dengan T yang sama sehingga susah untuk diprediksi T yang mana merupakan First dari E. (T + E | T)

First(T) adalah int dan ( tetapi untuk int ada 2 sehingga juga susah diprediksi int yang mana merupakan first dari T. (int | int * T)

Penyelesaian dengan Left Factoring:

Mengeluarkan prefix yang sama dalam produksi yang bisa mengakibatkan munculnya

ε-productions:

E → T + E | T menjadi E → T (+ E | ε ) => (dalam hal ini mengeluarkan T) sehingga membentuk:

E → T X

X → + E | ε

T → int | int * T | ( E ) menjadi T → int (* T | ε ) | ( E ) => (dalam hal ini mengeluarkan int) sehingga membentuk:

T → int Y | ( E )

Y → * T | ε

Setelah di left factoring maka untuk menentukan First dari suatu grammar akan tidak keliru dan lebih mudah diprediksi dan diparsing.

www.binus.ac.id